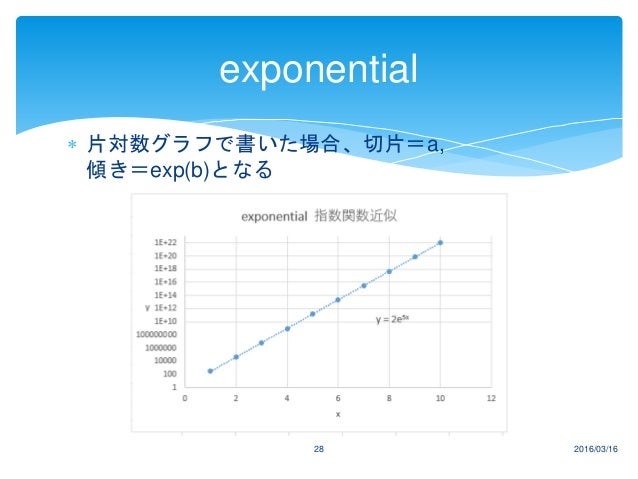
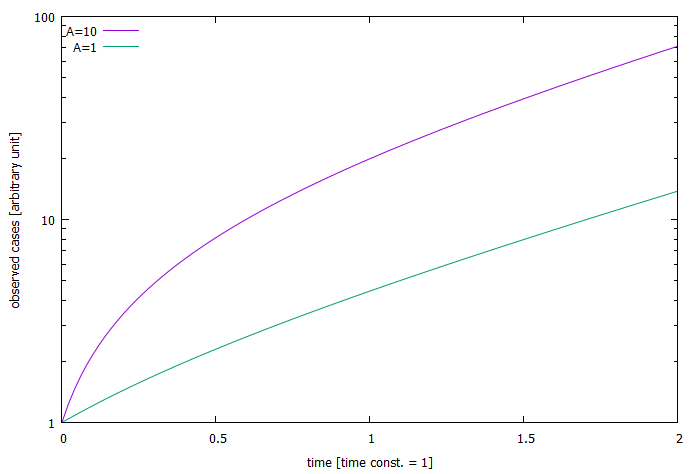
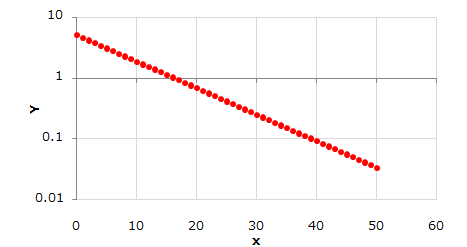
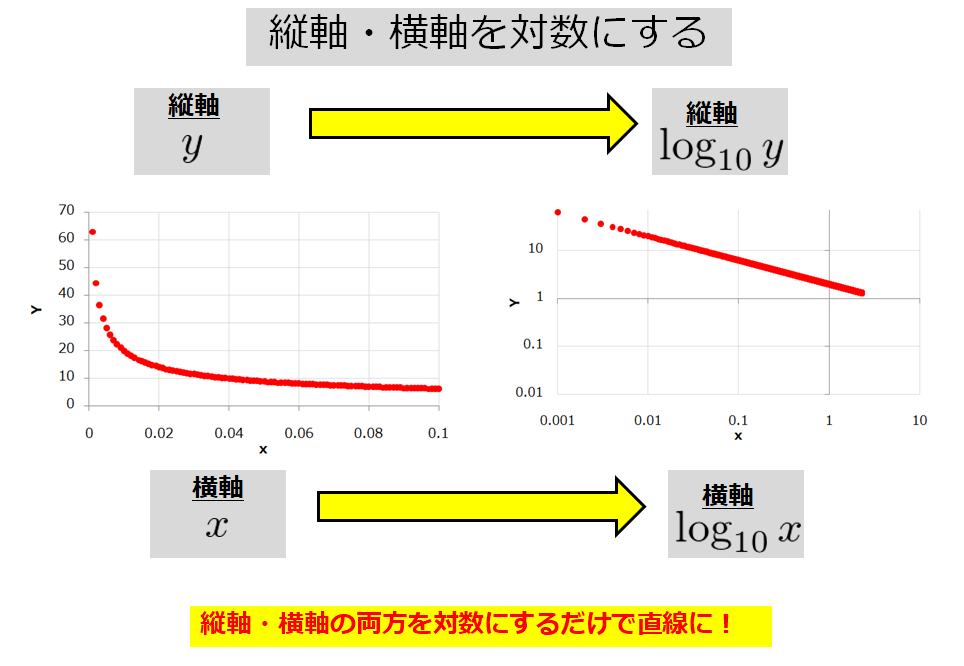
あとは,0dBから傾きが 時定数や整定時間とは 制御工学を初めて学ぶ人がまず読むべき参考書 ときの初期圧力であるq/sを 一定として,(2)式 を片 対数のグラフにプロットしたとき直線の傾きを表す量 (s/v)の 逆数(v/s)を 排気の時定数τp=v/sと いう 排気速度が大きければ(τpが小さければ)短 時間で目 的とする圧力に下がり,また,容 積が大きければ逆に時片対数グラフ(線形対数)の図2では指数関数である青線の が直線である。 図から横軸 が100増えると緑の縦軸 が約4増加しており傾きが004程度、切片は005程度と読み取れる。
半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方
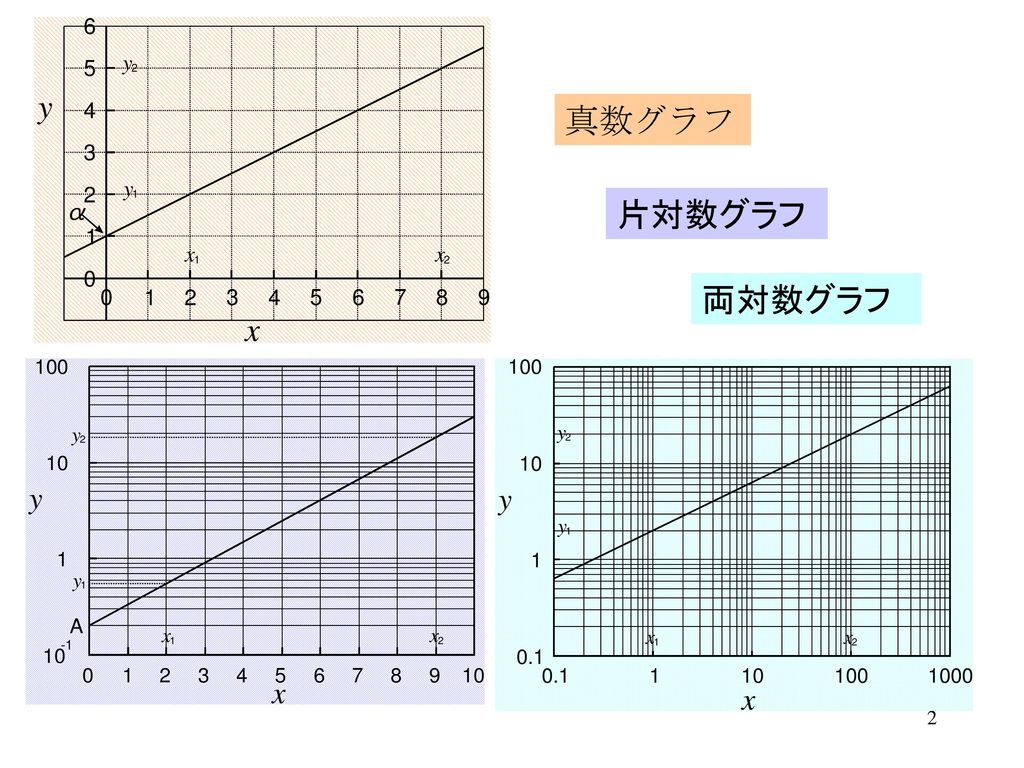
片対数グラフ 傾き 時定数
片対数グラフ 傾き 時定数-速度式と速度定数 両対数グラフにそのままプロット 課題 1 ※ 普通方眼紙および両対数グラフ用紙の両方で表示せよ (0, 27) グラフ用紙に作図した直線の傾きの読み取り方減衰振動や制振材料などの減衰特性を表す係数には、減衰比(ダンピングファクタ)、対数減衰率、損 失係数、q 値などがあります。それぞれの係数の定義や物理的な意味は後から説明することにして、こ こではまず、これらの係数の求め方を説明します。
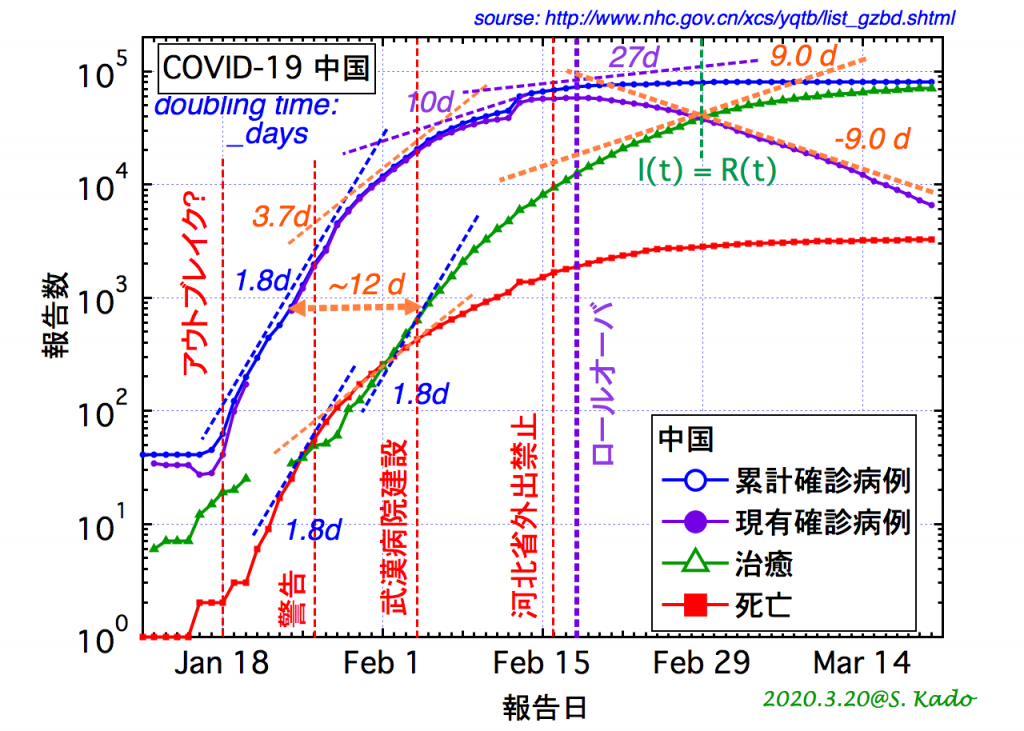



この感染は拡大か収束か 再生産数 R の物理的意味と決定 単純なモデル方程式に基づく行動変容の判断のために Rad It21
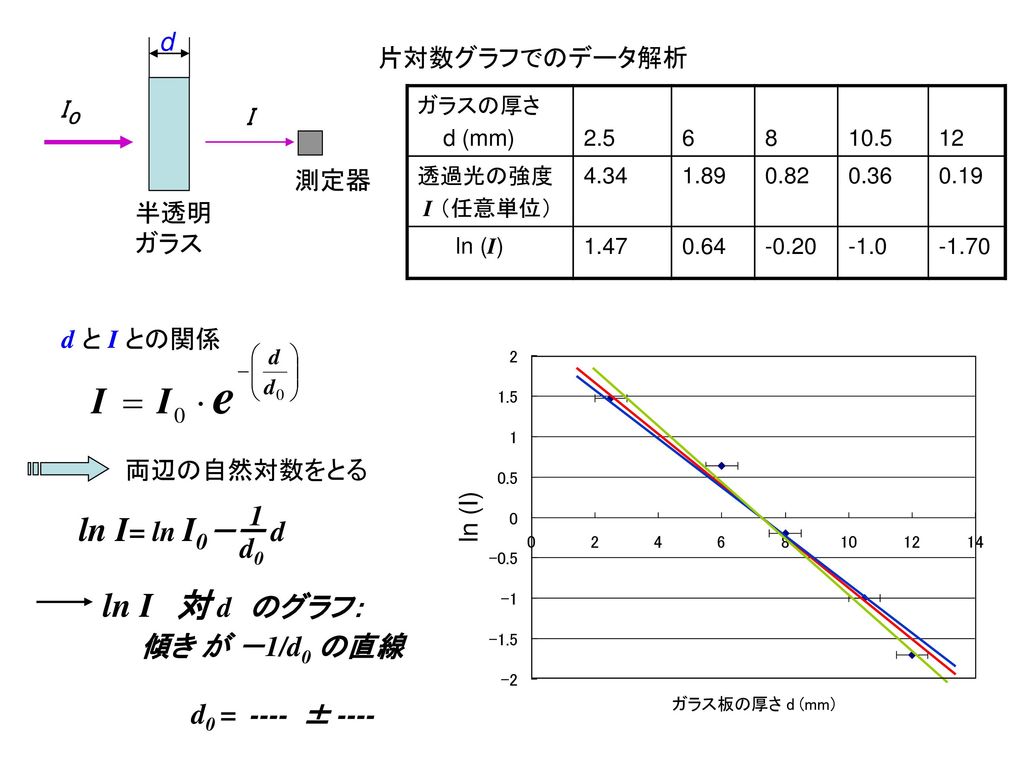
図8 片対数グラフ べき関数の式(3) を変形する。y = 10Y を代入し、両辺の10 の対数を取る。 y = 08x2 10Y = 08x2 Y = 2log 10 jxjlog 10 08 Y ≃ 2log 10 jxj Y とx は対数関数となり、図8 のべき関数を表す赤線は線形線形グラフ(図7)の対数関数(緑線)と近い上に 凸の曲線になっている。F とした片対数グラフで表しています。ダイオード の順方向特性には以下のような特長があります。 ・電流が微小でも電圧降下がある。 ・シリコンによって作られているダイオードでは温度係数が負 とために、地下水流出成分の分離時定数Tc を求める。ハイドログラフ低減部曲線を 片対数紙にプロットすると、低減部が2 ~3本の直線で近似できる。勾配がもっ とも緩やかな直線部の傾きをαとすれ ば、Tc =1/ αで決定される。
CRハイパスフィルタは、コンデンサと抵抗のみで構成されたハイパスフィルタです。 入力電圧の高周波成分を通過させ、低周波成分を遮断します。 後ほど導出方法など詳細に説明しますが、 CRハイパスフィルタの『伝達関数』,『ゲイン』,『カットオフRc直列回路の時定数について 先日学生実験を行ったのですが、片対数用紙で作成したグラフの傾きから時 定数 CRの値を求める問題が解けません。 最小二乗法を用いてグラフの傾きを求めて、そこから計算してみたのです下の図では、対数 log 10 = 1を長さ100mmに対応させて表している。 例 log5はA点の位置に点を取れば、log5=になる。B点は log40 である。片対数は縦軸、横軸の目盛り方がどちらか一方が対数目盛であり、両軸とも対数軸の場合は両対数と言っている。
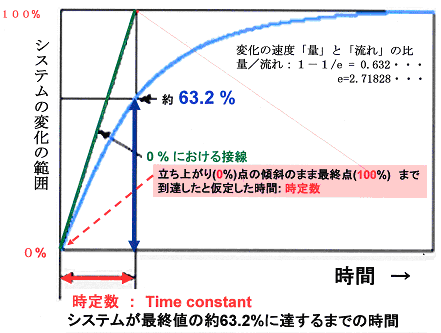
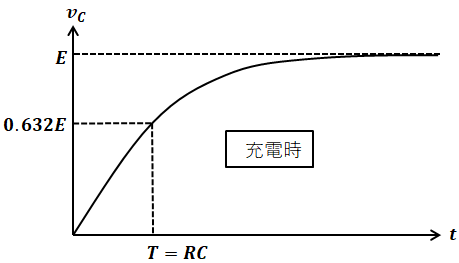
時定数 τ 積分回路に直流定電圧(例えば、電池)を入力(Vi)した時、出力波形(Vo)が立ち上がり、63%の高さまで上昇するまでの時間が積分回路の時定数(τ)に相当します。 ≪時定数τと応答≫ ①時定数(τ)が短い(小さい) : 急激に上昇する →応答が速いとなる。比例定数μ(次 元はhr1)を 比増殖速度と呼 ぶ。 (111)式 をμ=一定という条件で解けば容易に, (112) または, (113) である。n0はt=0に おける菌体数*)である。 (112)式 から明らかなように片対数紙の縦軸にnを, 横軸にtを とれば直線となる。よってμ=一定の片対数グラフ(かたたいすうぐらふ、semilog graph) とは、グラフの一方の軸が対数スケール(縦を対数スケールとすることが多い)になっているグラフである。 極端に範囲の広いデータを扱える。通常の目盛(線形スケール)の軸を範囲の狭いデータに、対数スケールの軸は極端に範囲の広い



片対数グラフの傾きと切片の求め方を教えてください グラフが見 Yahoo 知恵袋




06 号 自然対数仕様の刻み線を備えた対数方眼 Astamuse
なぜ片対数グラフ(あるいは両対数グラフ)を使うと直線になるのか? y になっているグラフのことを指しています。 ↑これが 片対数グラフ です。 y軸の目盛りの間隔が等間隔ではないですよね。 昔、先生に「このよくわからない紙に計測した点を 時定数の求め方について質問です。 コンデンサの電圧をVcとしたとき、正弦波交流波形において Vc=V×e^(t/RC) となると思うのですが、これを片対数グラフにプロットして傾きから時定数を求めたいです。)、湾曲点の傾きが必要。 線形グラフ 片対数グラフ 片対数グラフ 生体では陰性変時作用を心停止の時点まで追跡することは



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方



Zabbix 3 0 の予測機能のための数学的理解
手順1 片対数グラフを用意 y = e x のデータとグラフを作ります. 実際は,次に示すグラフが実験などから得られたという想定です. Copied!片対数グラフとは、「x軸: 普通の目盛 、y軸: 対数目盛 」や「x軸: 対数目盛 、y軸: 普通の目盛 」のようにx軸またはy軸の 片方 が対数目盛となっているグラフのことを指します。 片対数グラフは英語では「SemiLog Plot」または「SemiLog Graph」と書きます。Last と終末消失相の傾き(λ z)からC last /λ z として外挿する(図 C)。λ z は 最終測定点から数点の片対数グラフ上での直線部分を用いて、最小2 乗法で計算する。単 回投与データの場合、AUC は最終測定点までの値(AUC last あるいはAUC 0T)と無限時間




片対数グラフ 両対数グラフの傾きの意味 高校数学の美しい物語




この感染は拡大か収束か 再生産数 R の物理的意味と決定 単純なモデル方程式に基づく行動変容の判断のために Rad It21
さらに,ln(V0 v) vs t で得られる傾きと,片対数グラフ用紙でV0 v vs t の傾きは同じであるので,片対数のグラフ用紙にV0 v をプロットするのが,最も簡単な方法で あろう。片対数のグラフ用紙とは縦軸に01, 1, 100, 1000, を等間隔に目盛ったものである(図3発展片対数方眼紙で、縦軸に電流、横軸に時刻をとると、 log10I=log10I0-(log10e/RC)t のグラフになる。このグラフの傾き(縦は大きな1マスが1、横軸は普通に読む)=-log10e/RC より、Cを片対数グラフで直線を引いて時定数を求めることができる。これは何故か?また、誤差を考慮 すると、その直線はどのように引くといいだろうか? この測定の場合の片対数グラフ用紙の利点は何か? 図 コンデンサーの充放電の測定回路
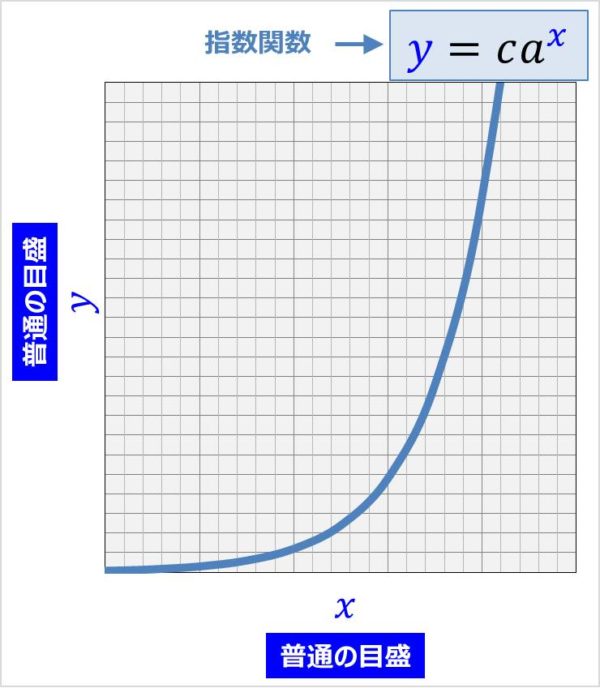



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説



国際物理オリンピック実験試験のシラバス 1 標準的な実験器具 装置が使える マニュアル無しで使える Ppt Download
• 片対数グラフで直線を引いて時定数を求めることが できる。これは何故か?また、誤差を考慮すると、そ の直線はどのように引くといいだろうか? • 傾きを求めるとき、最小2 乗法を用いなくても良い と指示されている理由を考えよ。 時定数の求め方について質問です。 コンデンサの電圧をVcとしたとき、正弦波交流波形において Vc=V×e^(t/RC) となると思うのですが、これを片対数グラフにプロットして傾きから時定数を求めたいです。片対数グラフの傾きから関数y=Aexp(Bx) の定数A, Bを求める方法 片対数グラフにプロットする事は、方眼グラフでlog 10 yを縦軸にとることに等しい。 したがって



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



2
片対数グラフの傾きの意味 片対数グラフ( x x x 軸が通常の目盛, y y y 軸が対数目盛)について説明します。 指数関数は片対数グラフに書くと直線になります。 そのため, 片対数グラフは,指数関数を図示するのに便利なグラフ と言えます。Rc直列回路の時定数(τ=cr)の導出 関連ページ 過渡現象とは 過渡現象について解説しています。過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象(電圧や電流などの時間的な変化)のことをいい、過渡現象は回路の状態が変化することによって起こります。緩衝溶液 緩衝溶液の効果を式のうえで見ていくことにしよう。 ha h a




片対数グラフ 両対数グラフの傾きの意味 高校数学の美しい物語



2
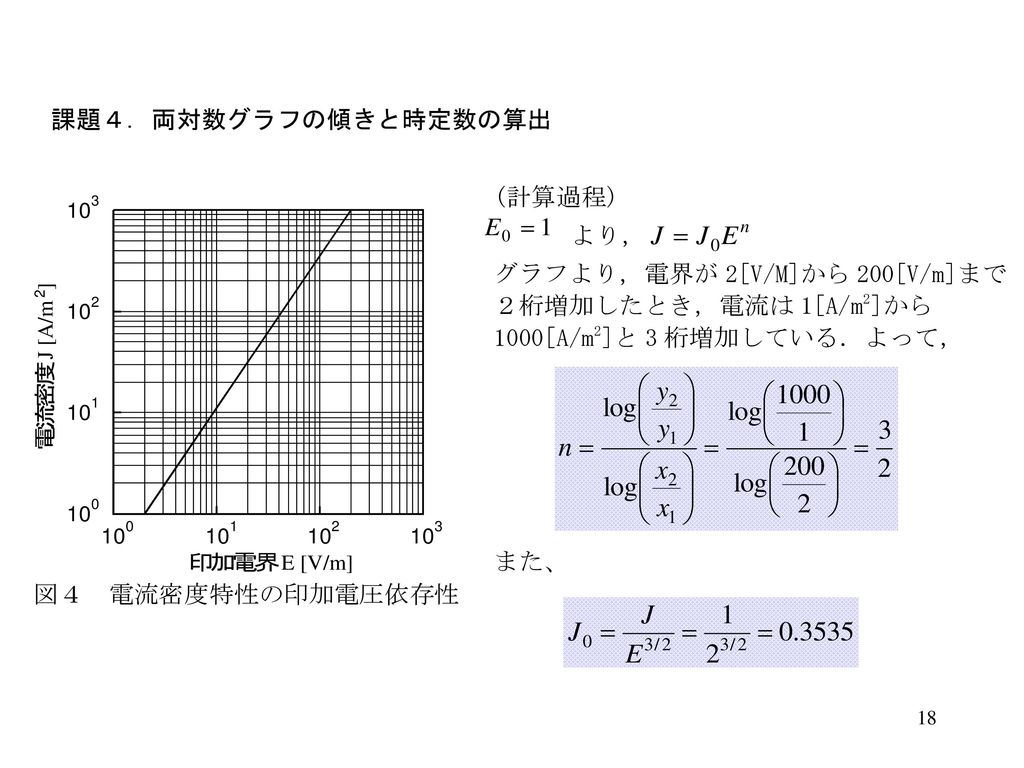
数k との間に片対数グラフ上で直線関係が認められた1)。 BDerby とMFAshby はn と他の実験定数との間に片対 数グラフ上での直線関係を指摘している2)。本研究は,応 力指数n と係数k の関係式k = BAn(A,B実験定数) がク ボード線図の描き方について解説 21年3月7日 周波数解析法として、ボード線図やナイキスト線図、ベクトル軌跡があります この記事では、ボード線図の書き方や意味について説明します この記事で出てくる"ゲイン"や"周波数伝達関数"、"位相"についてこの"oct" は対数目盛上での, ある値とその2 倍の値との間隔 を表す。よって, このグラフの長い方の直線部分(102 から2 102) で傾きを調べると, (傾き) = 69 40 2102 102 = 6151dB=oct 522 利得最小時の周波数 素子の定数から計算すると, 利得が0dB になる周波数



時定数の求め方について質問です コンデンサの電圧をvcとしたとき 正弦波 Yahoo 知恵袋



1



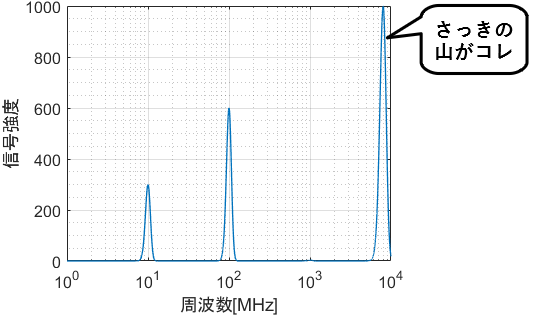
Yoh Tanimoto R 0 1 7 1 Gamma 4 T Co Rplkt3ahgk とすると 時定数の逆数は 4 1 7 1 5 7日ですが 6日かその倍の12日経ってからの傾きは日本とヨーロッパでやはり違うように見えます



情報機構 講師コラム



対数目盛を含むグラフ上での最小二乗法の実装 Codezine コードジン



2



電験三種 H28 理論 問10解説 電験三種 これでok




マルチチャンネルのデータ アクイジション システムの性能を高める ポイントは入力セトリング時間の最適化 アナログ デバイセズ



ある薬物300mgをヒトに静脈内投与したところ 下の片対数グ Yahoo 知恵袋




07 号 センサレスブラシレスモータの駆動装置 Astamuse



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方




類似問題一覧 臨床工学技士国家試験対策サイト



片対数グラフの傾きと切片の求め方を教えてください 左上の点は 0 Log Yahoo 知恵袋



電気基礎実験 グラフ処理 Ppt Download



高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ



Excelでの片対数グラフでの線形近似曲線の傾きの求め方がわかりません グラ Yahoo 知恵袋



この片対数グラフの傾きと切片は何を表しているのですか Yahoo 知恵袋



2



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方



片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾
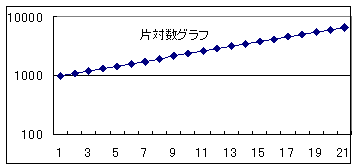



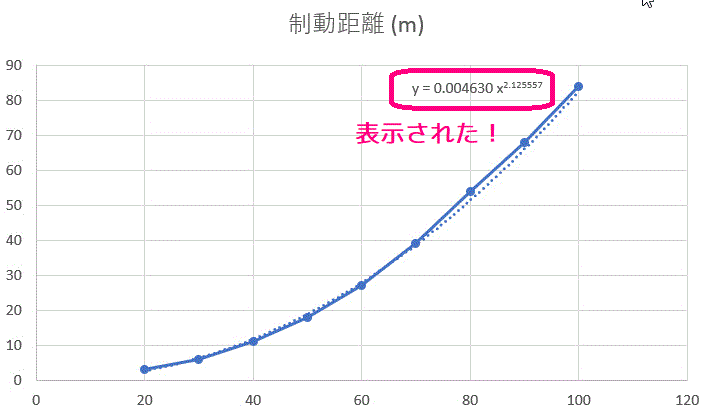
貝の成長 と マルサスの法則 と 株のチャート 変化の法則を片対数グラフで見る はじめに この前 対数グラフを学習した これは べき関数の変化が指数乗に比例している場合を見つけることだった だから両対数グラフで表すと




薬物動態 消失半減期t1 2とグラフの読み方




06 号 自然対数仕様の刻み線を備えた対数方眼 Astamuse
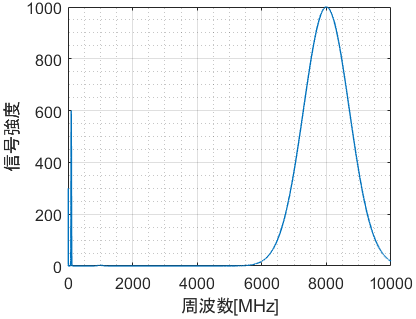



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説




線形コンパートメントモデルに基づいた解析 Yakugaku Lab
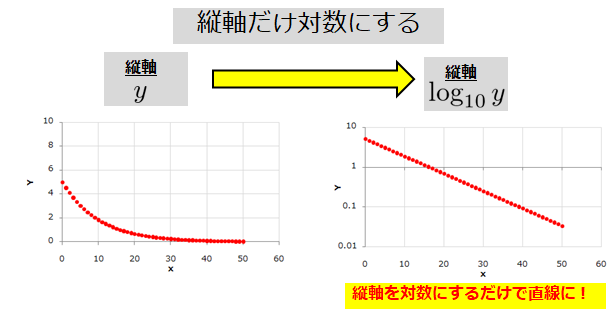



高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ




仮 変な対数グラフ
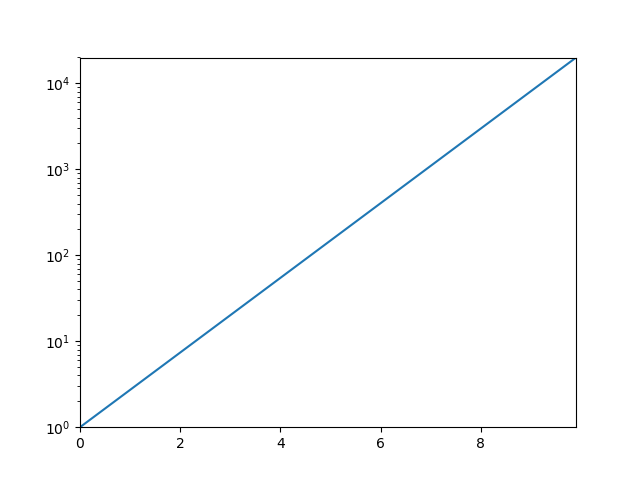



片対数グラフを読む Qiita



電気基礎実験 グラフ処理 Ppt Download




類似問題一覧 臨床工学技士国家試験対策サイト




対数 Wikipedia




13 号 バッチ式分離を用いた多相流量計 Astamuse



2




片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾




片対数グラフでこのような形になるとは どういうことなのでしょうか 工学 教えて Goo



高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ
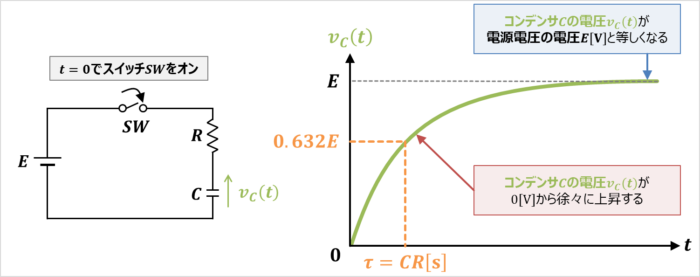



Rc回路の時定数 求め方や単位などを詳しく解説
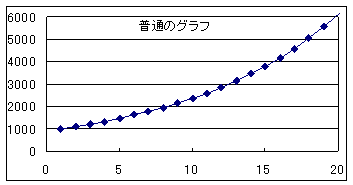



貝の成長 と マルサスの法則 と 株のチャート 変化の法則を片対数グラフで見る はじめに この前 対数グラフを学習した これは べき関数の変化が指数乗に比例している場合を見つけることだった だから両対数グラフで表すと




対数目盛を含むグラフ上での最小二乗法の実装 Codezine コードジン
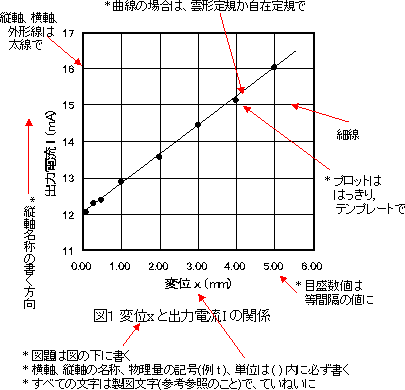



測定値の表し方
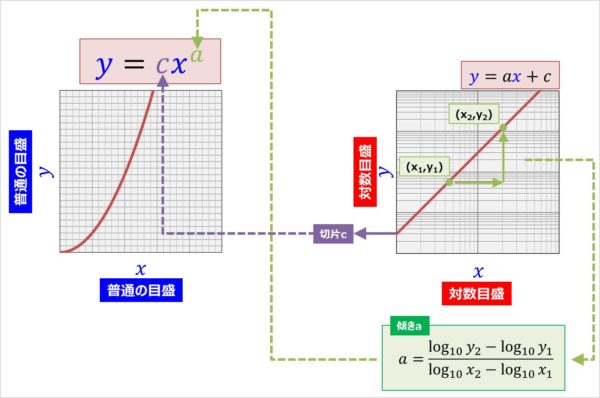



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説




06 号 自然対数仕様の刻み線を備えた対数方眼 Astamuse




電解コンデンサの時定数についてです コンデンサ充電時の電圧の変化 物理学 教えて Goo




片対数グラフを読む Qiita



3 対数グラフの利便性




対数グラフを計算式に直す方法 学校で習ったと思うのですがすっかり忘れてし Okwave



1




単位とスケール



名城大学 小澤研究室
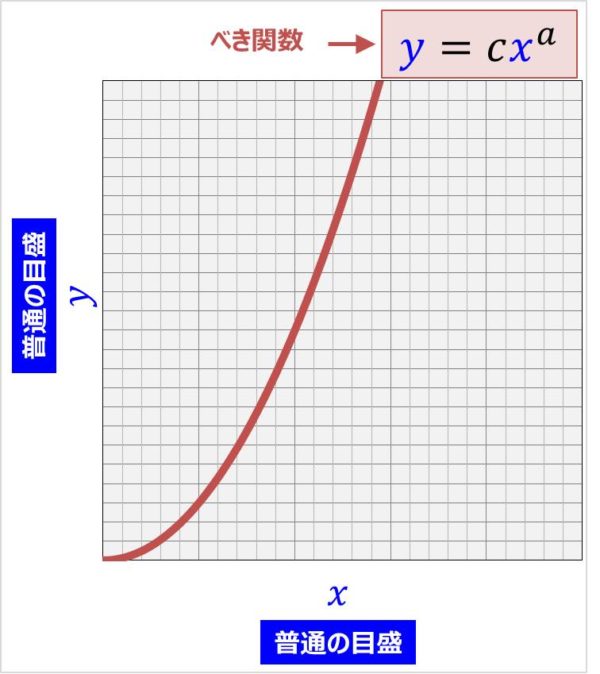



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説
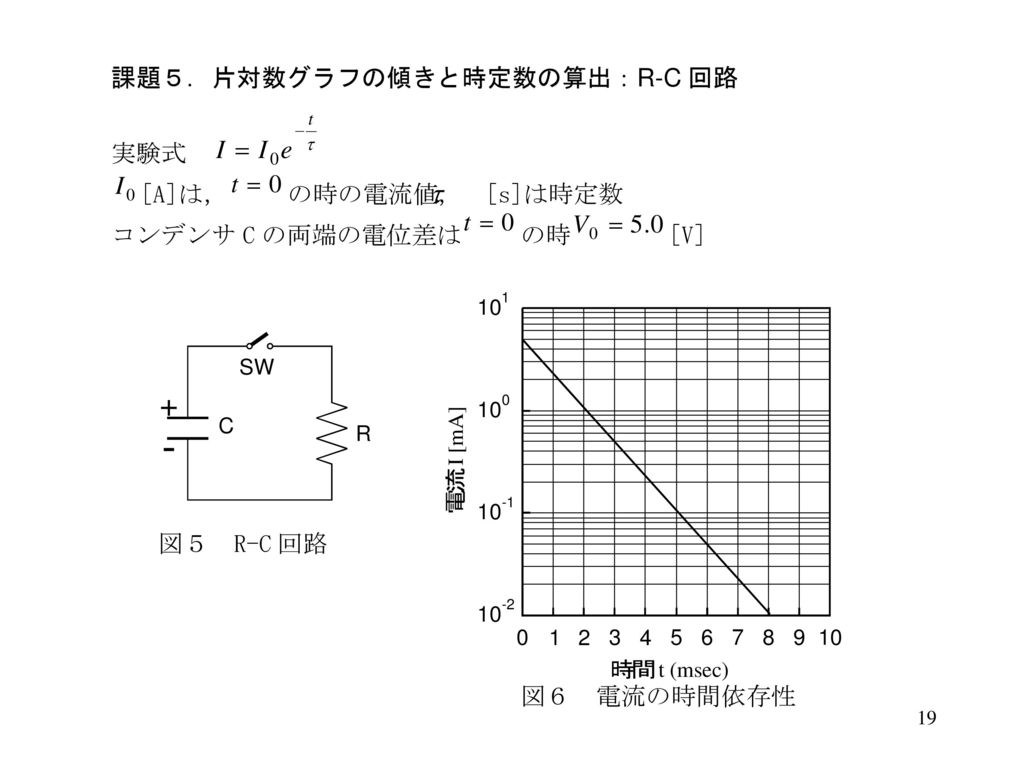



電気基礎実験 グラフ処理 Ppt Download




係数図法プログラム 事業分野別論文 宇宙システム分野 技術情報 三菱スペース ソフトウエア



スライド 1



自然対数仕様の刻み線を備えた対数方眼



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方



実験 コンデンサーの放電曲線
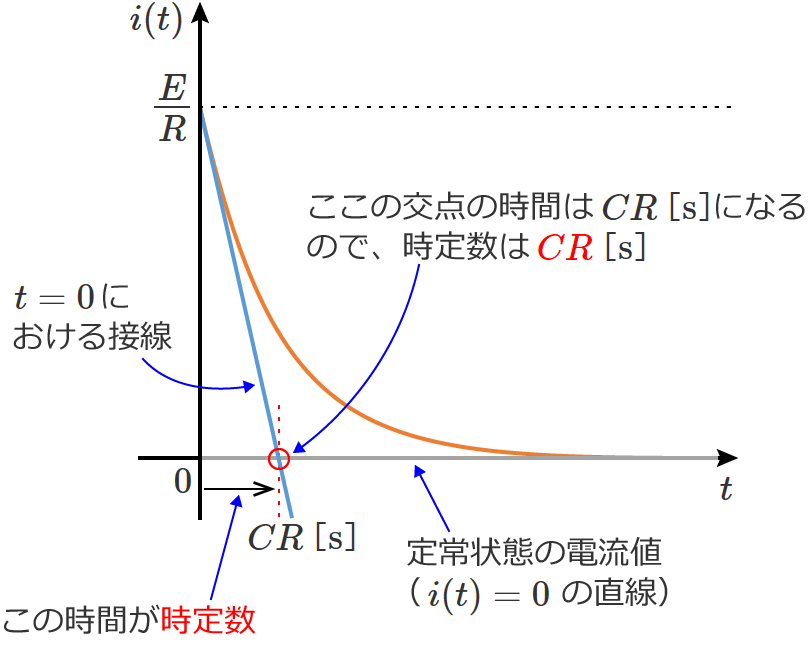



Rc直列回路の時定数 T Cr の導出



1




両対数グラフ Emanの物理数学
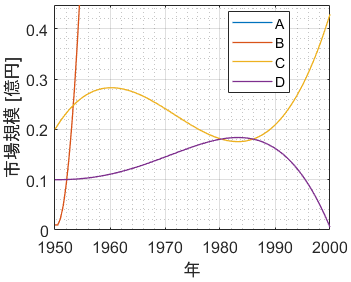



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説
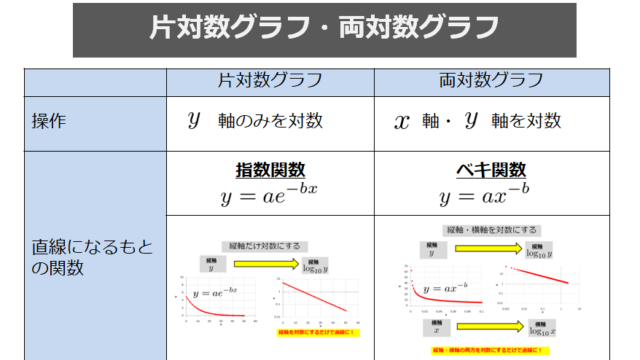



高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ



実験 コンデンサーの放電曲線



レポート作成上のヒント
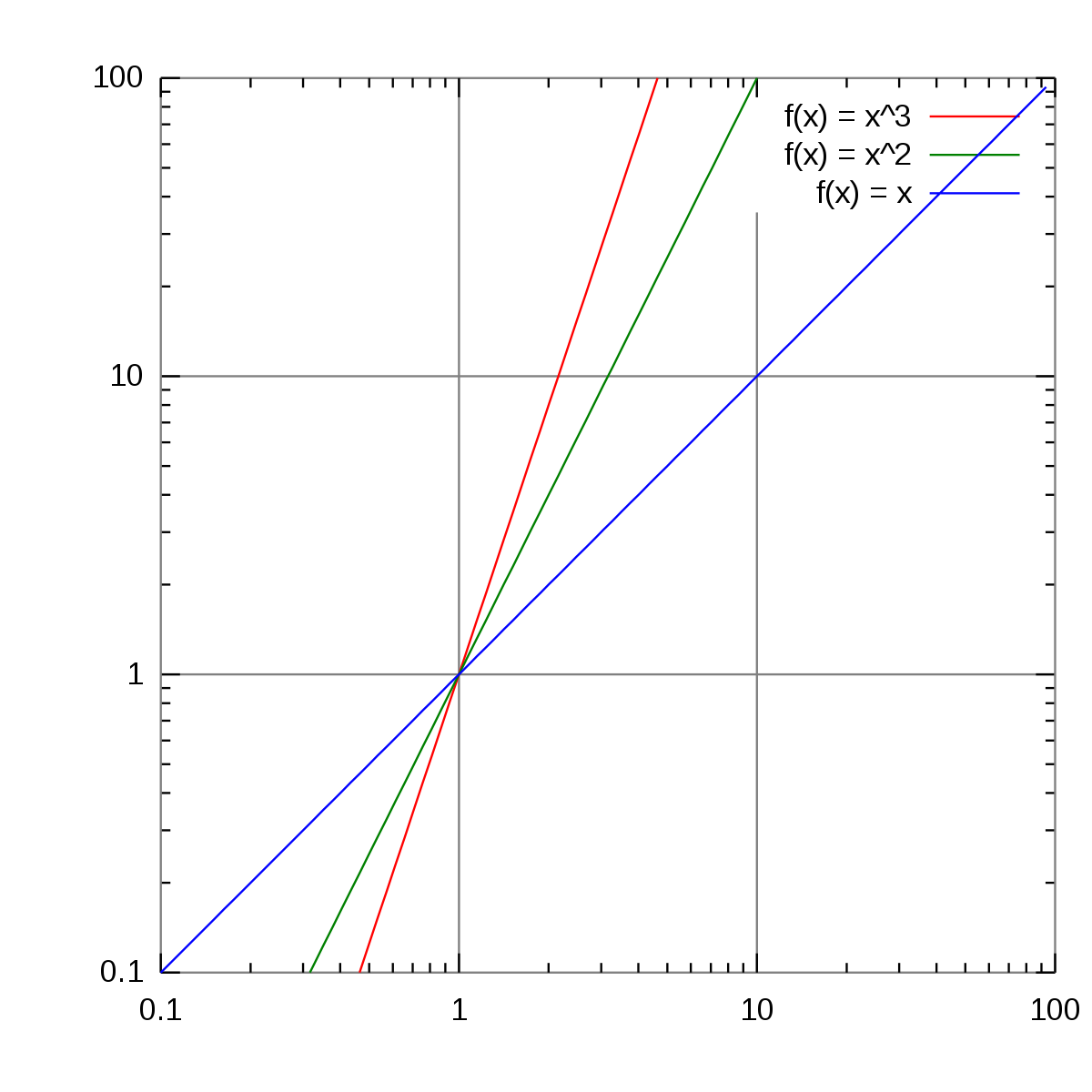



両対数グラフ Wikipedia



1
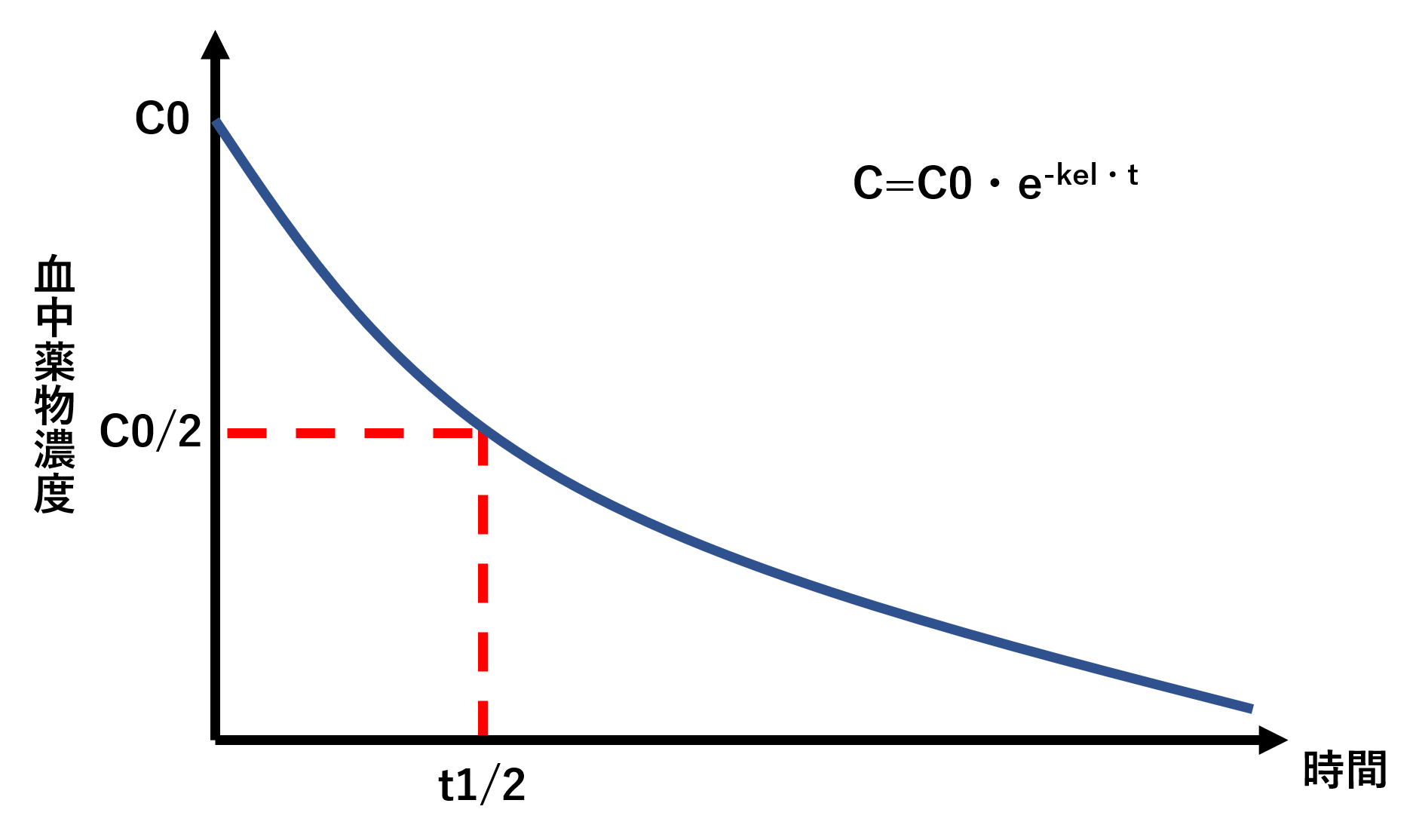



薬物動態 消失半減期t1 2とグラフの読み方




問題一覧 臨床工学技士国家試験対策サイト
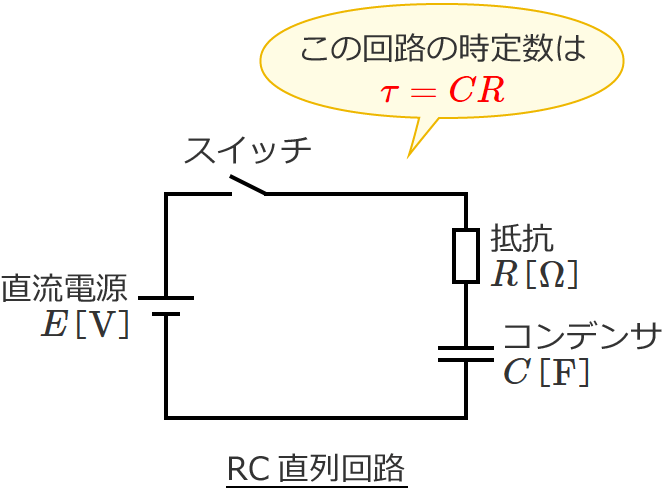



Rc直列回路の時定数 T Cr の導出



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方



最小二乗法 指数近似と累乗近似 最小二乗法のうち 指数近似と累乗近似をする場合について考えてみましょう 世の中の現象は 決して線形的な関係ばかりではありません むしろ 指数関数的な変化や 累乗関数的な変化になることが多いものです
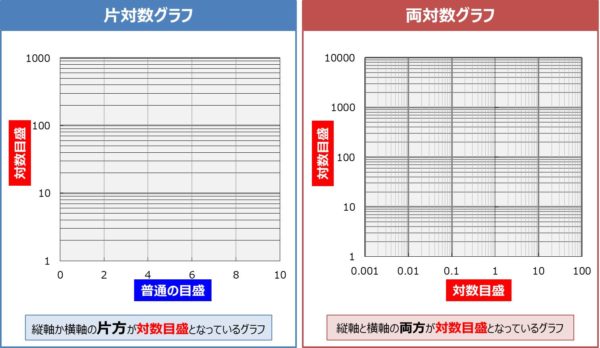



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説
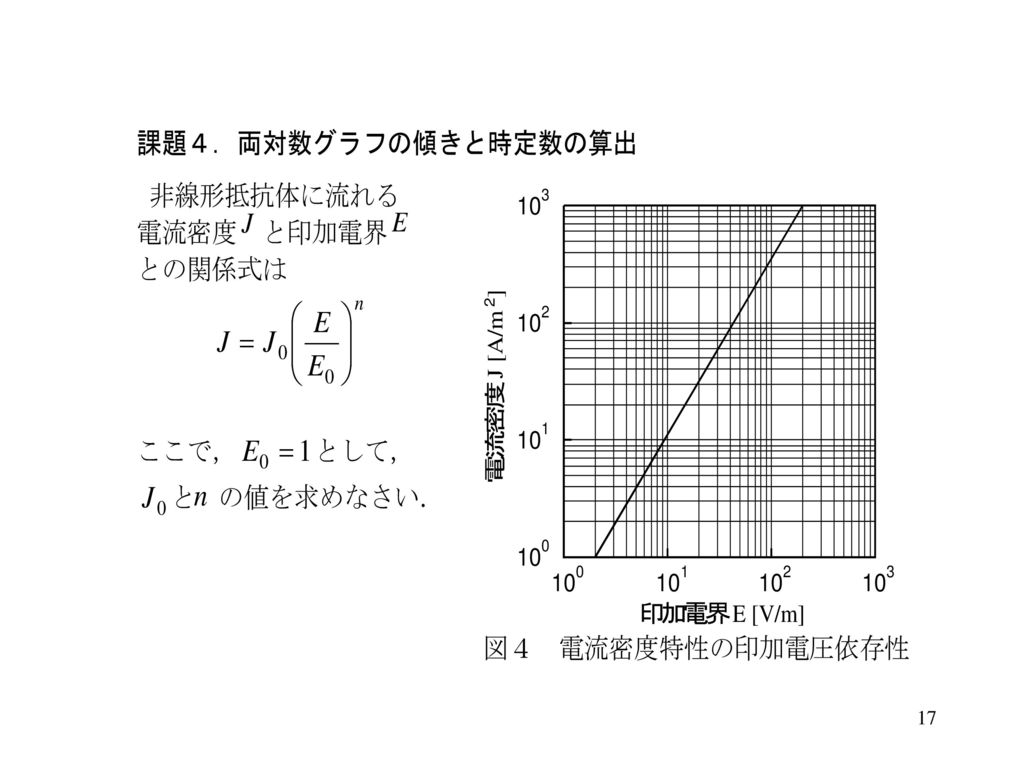



電気基礎実験 グラフ処理 Ppt Download
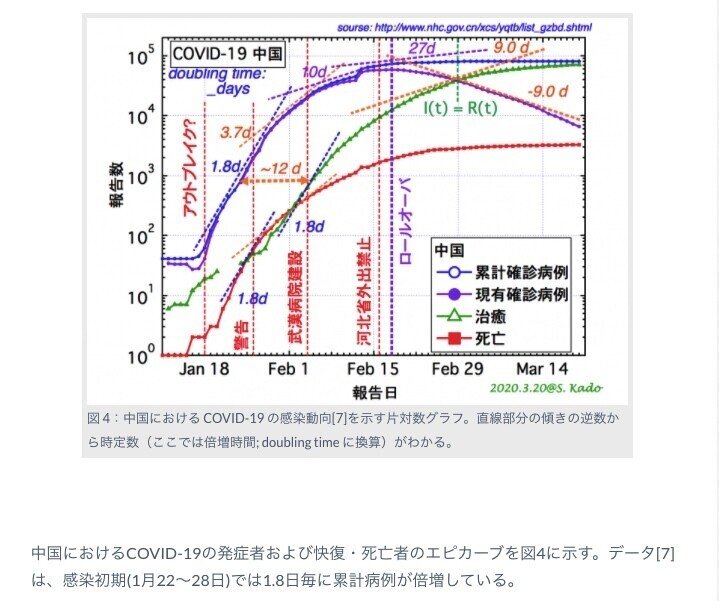



新型コロナ 素人 の物理学者たちが声を上げる理由 小宮山亮磨 Note
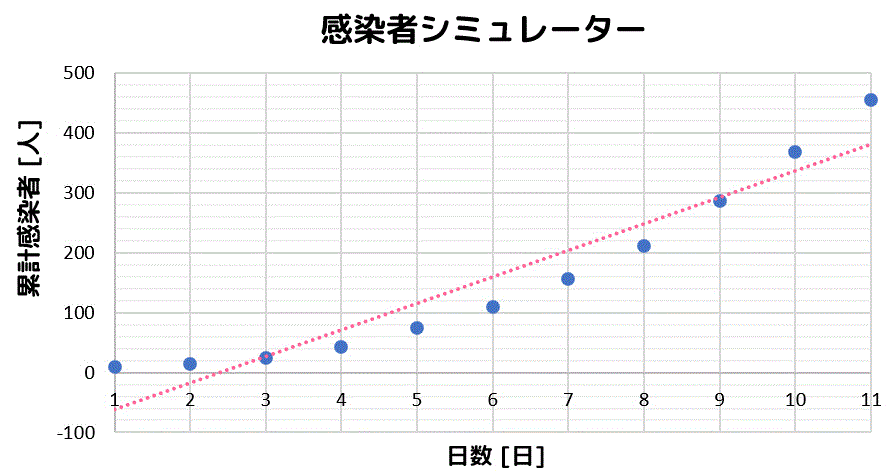



片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾
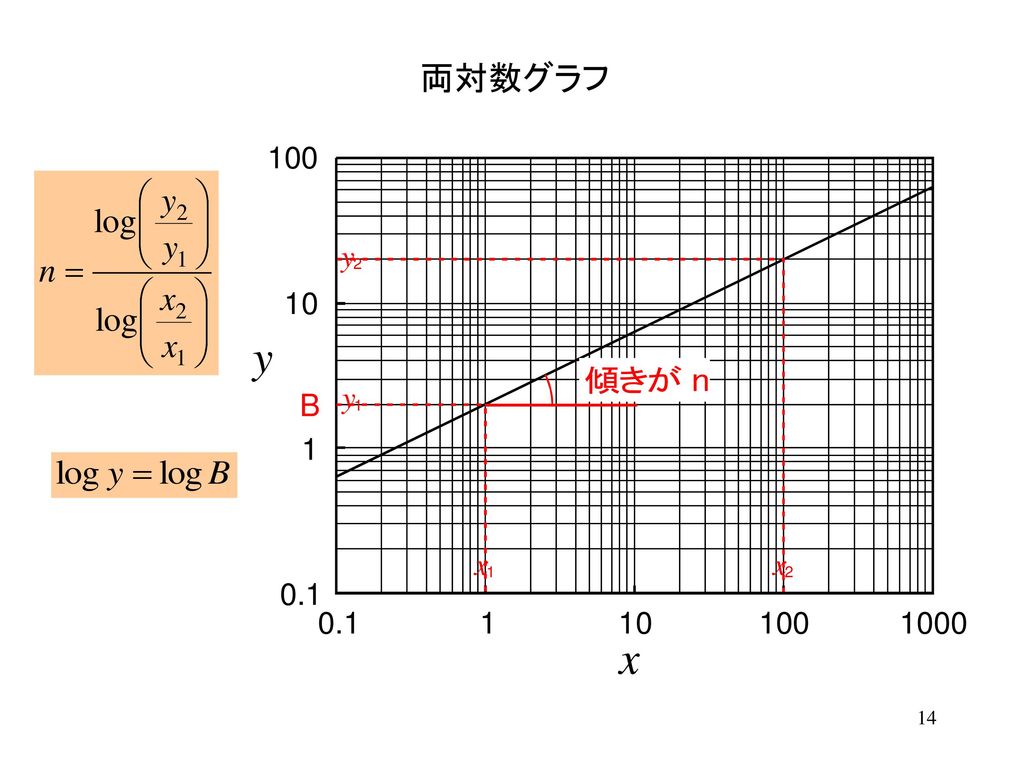



電気基礎実験 グラフ処理 Ppt Download




片対数グラフ 両対数グラフの傾きの意味 高校数学の美しい物語



名城大学 小澤研究室




類似問題一覧 臨床工学技士国家試験対策サイト



両対数グラフ Wikipedia



電圧減衰の指数関数曲線を片対数グラフに直線の形であらわした時 直線 Yahoo 知恵袋




世知辛さ単調増加の法則について 観測された感染者数に関する覚書き




06 号 自然対数仕様の刻み線を備えた対数方眼 Astamuse



実験結果の整理




線形グラフと片対数グラフの違いとphに対数が使われる訳
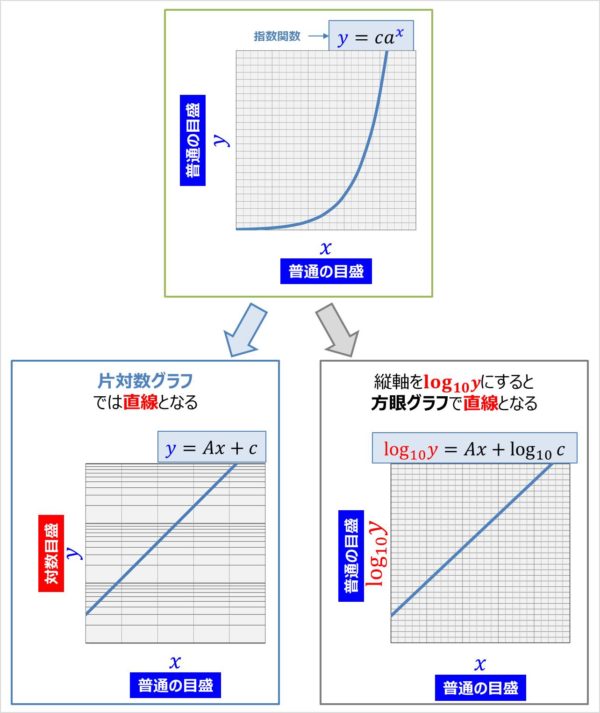



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説
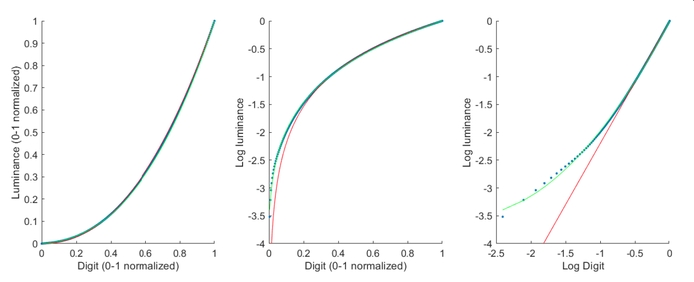



ディスプレイの色校正について



実験結果の整理
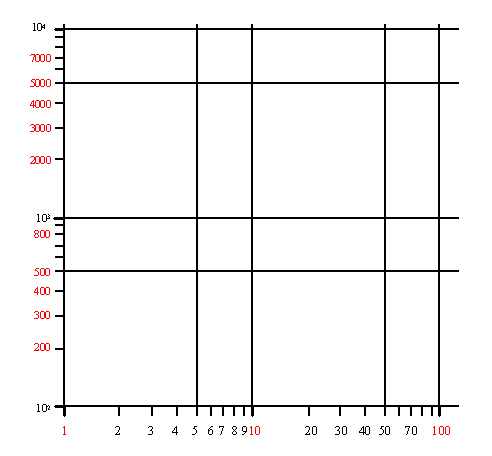



測定値の表し方
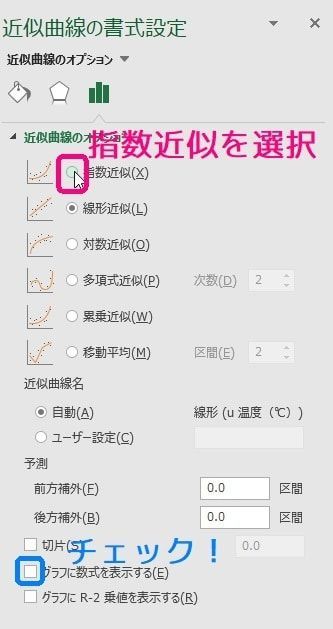



片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾




両対数グラフの直線の近似式の求め方は 両対数グラフで直線になったグラフ Okwave



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方
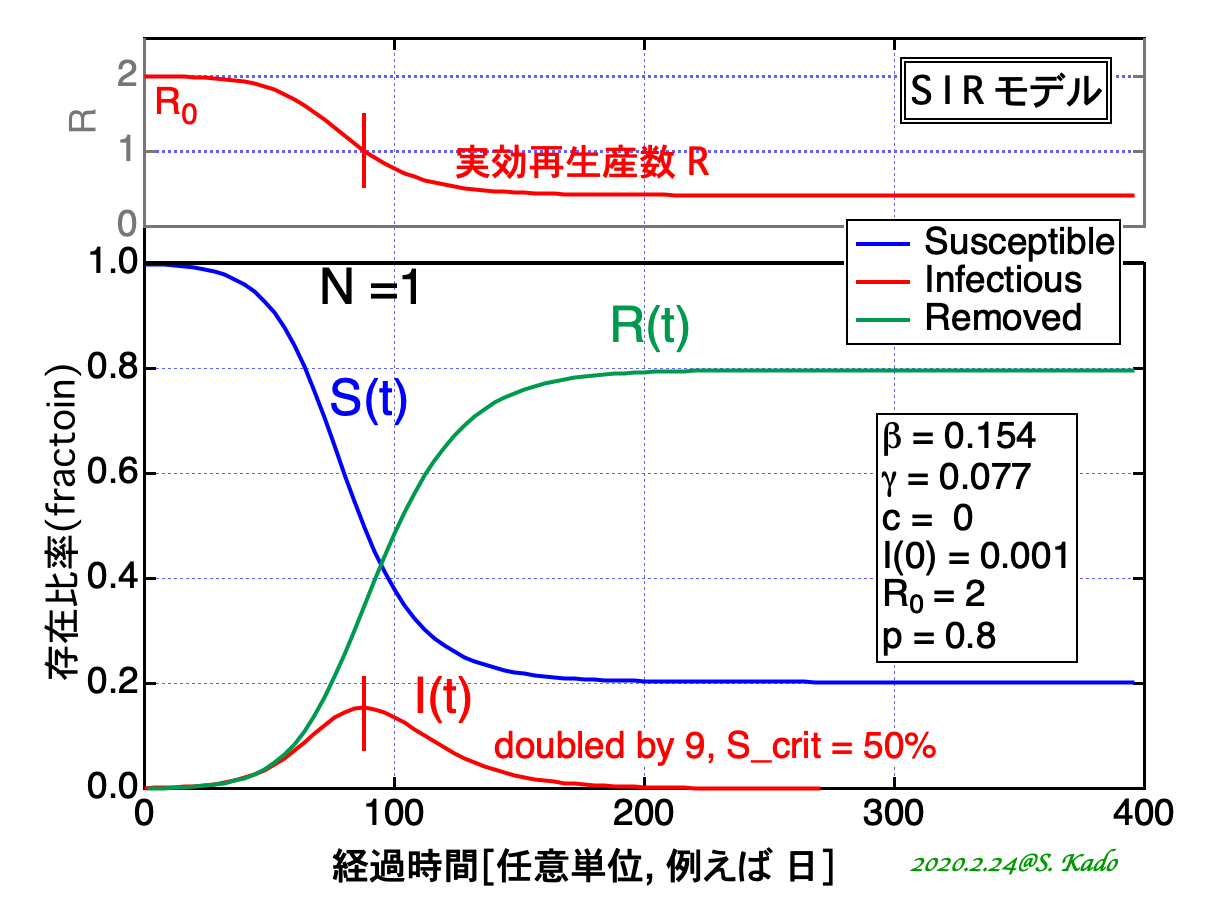



この感染は拡大か収束か 再生産数 R の物理的意味と決定 単純なモデル方程式に基づく行動変容の判断のために Rad It21



0 件のコメント:
コメントを投稿