Solution Given the sum of zeroes (s), sum of product of zeroes taken two at a time (t), and the product of the zeroes (p), we can write a cubic polynomial as \p\left( x \right) k\left( {{x^3} S{x^2} Tx P} \right)\ k can be any real number Its value will have no effect on the zeroes In this particular case, the answer will be Product of the zeros = × = = Example 4 If α and β are the zeros of ax2 bx c, a ≠ 0 then verify the relation between the zeros and its coefficients Sol Since a and b are the zeros of polynomial ax 2 bx c Therefore, (x – α), (x – β) are the factors ofSum of pair products = αβ α(αβ) β(αβ) = αβ (αβ)² = ᶜ/ₐ b²

A B G Are Zeroes Of Cubic Polynomial Kx3 5x 9 If
α β γ are zeroes of cubic polynomial kx3 – 5x 9. if α3 β3 γ3 = 27 find the value of k
α β γ are zeroes of cubic polynomial kx3 – 5x 9. if α3 β3 γ3 = 27 find the value of k- The equation is x^36x^21=0 Let's rewrite the equation as x^30x^26x^11*x^0=0 If alpha, beta and gamma are the roots of this equation, we have (xalpha)(xbeta)(xgamma)=0 (x^2alphaxbetaxalphabeta)(xgamma)=0 x^3(alphabetagamma)x^2(alphabetagammabetaalphagamma)xalphabetagamma=0Q10 If α and β are the zeros of the quadratic polynomial f(x) = 2x² 5x 7, find a polynomial whose zeros are 2α 3β and 3α 2β?



Xdocs Pl
If α and β are the zeroes of the quadratic polynomial P(x) = Kx 2 4x 4 such that α 2 β 2 = 24, find the value of K Since, α and β are the zeroes of the quadratic polynomial P(x) KxIf α, β are the zeroes of the quadratic polynomial x^2 kx = 12, such that α – β = 1, find the value of k asked in Polynomials by Anika01 ( 571k points) polynomialsFind all the zeroes of the polynomial 2xcube xsquare 6x 3 if 2 of its zeroes are √3 and √3 IF one of the zeros of quadratic polynomial is f(x)=14x²42k²x9 is negative of the other, find the value of k
αβ = ᶜ/ₐ} Given the roots of the new one, evaluate same summations in terms of the original equation eg roots of α,β and αβ in a cubic, giving sum of roots = αβ(αβ) = ⁻²ᵇ/ₐ ; Sir I have a doubt and plz solve it very early as exam is going to start on thrusday Please solve question Question – If alpha, beta are the zeroes of polynomials x^28x6 , form a polynomial whose zero are alpha – beta , alphabeta Here, α β = 0, αβ = √5 Thus the polynomial formed = x 2 – (Sum of zeroes) x Product of zeroes = x 2 – (0) x √5 = x2 √5 Example 6 Find a cubic polynomial with the sum of its zeroes, sum of the products of its zeroes taken two at a time, and product of its zeroes as 2, – 7 and –14, respectively Sol
α,β and γ are zeros of cubic polynomial and are in AP So, Let β=a ;Example 2 Find all real zeros of the polynomial P(x) = 2x4 x3 – 6x2 – 7x – 2 Solution Step 1 First list all possible rational zeros using the Rational Zeros Theorem For the rational number p q to be a zero, p must be a factor of a 0 = 2 and q must be a factor of a n = 2 Thus the103 Questions found for Class 10 Maths Polynomials find a cubic polynomial with the sum, sum of its products of its zeroes taken two a time and the product of its zeroes as 3 , 8 and 2 respectively Asked by vikas mahajan find the zeroes of 4 root 3 x2 5 x 2 root 3 and verify the relation between the zeroes and cofficient of polynomial




If 2 And 3 Are Zeroes Of Polynomial 3x 2 2kx 2m Then Fin




A B Y Are The Zeroesof Cubic Polynomial Kx3 5x 9 Ifa3 Y3 27
If α, β Are the Zeros of the Polynomial F(X) = Ax2 Bx C, Then 1 α 2 1 β 2 = We have to find the value of `1/alpha^21/beta^2` Relationship Between Zeroes and Coefficients of a Polynomial video tutorial ; Write its truth value Write the contrapositive of the statement 'If a number is divisible by 9, then it is divisible by 3' Given below is a pair of statementsCombine these two statements using "if and only if"p If a rectangle is a square, then all its four sides are equalq If all the four sides of a rectangle are equal, then the√70以上 α β γ are zeroes of cubic polynomial kx3 – 5x 9 if α3 β3 γ3 = 27 find the value of k blogjpmbaher6w7 If α and β are the zeros of quadratic polynomal 2x25x7 , find a polynomial whose zeros are 3α2β and 2α 3β asked in Class X Maths by akansha




Intellect Guidance Centre Near Shiv Mandir Surendra Gali Jora Phatak More Dhansar Dhanbad Dhanbad 21



Xdocs Pl
Sum of zeroes = α β = 0 Product of zeroes = α β = √5 ∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly Exercise 22 Page 33 as 𝑥2 – (αβ)x αβ = 0 √𝑥2 – (0)x 5 = 0 Thus, 𝑥2 √ 5 is the quadratic polynomialα=a−d & γ=ad Polynomial =x 3−12x 244xc Sum of roots = 1−(−12) =12 So, a−daad=12 3a=12 a=4 Sum of products of two consecutive roots =44If the zeroes of the cubic polynomial f(x) = kx38x2=5 are alphabeta, alpha and alphabeta then find the value of k Get the answer to this question and




A B G Are Zeroes Of Cubic Polynomial Kx3 5x 9 If




16 A B G Are Zeroes Of Cubic Polynomial Kx3 5x 9 Ifa3 G3 27 Findthevalueofk
Answer (1 of 2) x³ 5x – 2 a=1, b=0, c=5, d= 2 Comparing we get α βγ = b/a=0 αβ αγβ γ=c/a=5 αβγ=d/a = 2 Since α,β,γ are zeroes of given If α and β are zeroes of the quadratic polynomial 𝑥2 − 6𝑥 𝑎, find the value of if 3𝛼 2𝛽 = s Class 10 , Maths , Polynomials Asked by ryanThe cubic polynomial should be in the form of ax3 bx2 cx d, where = – Coefficient of x2/ coefficient of x3 The sum of the product of zeros, αβ βγ αγ is c/a = Coefficient of x/Coefficient of x3 The product of zeros



If Alpha Beta Gamma Are Zeros Of Cubic Polynomial X 3 5x 2 What Is The Value Of Alpha 3 Beta 3 Gamma 3 Quora




12 A B G Are Zeroes Of Cubic Polynomial Kx3 5x 9 If A3 G3 27 Find The Value Of K Brainly In
Zeros of polynomials (with factoring) common factor When a polynomial is given in factored form, we can quickly find its zeros When it's given in expanded form, we can factor it, and then find the zeros!Linear, quadratic and cubic polynomials can be classified on the basis of their degrees A polynomial of degree one is a linear polynomial For example, 5x 3 A polynomial of degree two is a quadratic polynomial For example, 2x 2 x 5 Aα=a−d & γ=ad Polynomial=x3−12x244xc Sum of roots=1− (−12) =12 So,a−daad=12 3a=12a=4 Sum of products of two consecutive roots=44 a (a−d)a (ad) (a−d) (ad)=44a2−ada2ada2−d2=443a2−d2=443 (4)2−d2=44d2=48−44=4d=±2 So,



Ayazsir Com




If Alpha Beta Gamma Are Zeros Of Cubic Polynomial X 3 5x 2 What Is The Value Of Alpha 3 Beta 3 Gamma 3 Quora
39 32 α, β, γ are zeroes of cubic polynomial kx3 – 5x 9 If α3 β3 γ3 = 27, find the value of k SOLUTION 40 33 Two zeroes of cubic polynomial ax3 3x2 – bx – 6 are –1 and –2 Find the third zero and value of a and b SOLUTION 41 34 α, β, γ are zeroes of cubic polynomial x3 – 12x2 44x c If α, β, γ are in AP, find the value of cI f α and β are the zeros of polynomial x2 5x k such that α β =1 find the value of k asked in Class X Maths by akansha Expert ( 78k points) 2 votes Transcript Ex 24, 3 If the zeroes of the polynomial x3 – 3x2 x 1 are a – b, a, a b, find a and b For a cubic Polynomial p(x) = ax3 bx2 cx d With zeroes α, 𝛽 and γ We have 𝛂 𝛽 𝛄 = (−𝒃)/𝒂 𝛂"𝛽" 𝛽𝛄 𝛄𝛂 = 𝒄/𝒂 𝛂"𝛽" 𝛄= (−𝒅)/𝒂 Now, p(x) = x3 − 3x2 x 1



Xdocs Pl



Xdocs Pl
Ex 22, 1(i)Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficientsx2 – 2x – 8Let p(x) = x2 – 2x – 8 Zero of the polynomial is the value of x where p(x) = 0Putting p(x) = 0x2 – 2x – 8 = 0We find roots using splittQ11 If one of the zeros of the cubic polynomial x3 ax2 bx c is 1, then what will be the product of the other two zeros?(6) If α and β are the zeros of quadratic polynomial x2 3x 5, find the value of α3 β3 (7) If α and β are the zeros of polynomial x2 5x k, such that α2 β2 = 13 Find the value of k (8) If α and β are the zeros of polynomial x2 10x k, such that α β = 2 Find the value of k Choose correct answer(s) from given choice




Intellect Guidance Centre Posts Facebook




Polynomials 1 Pdf Polynomial Factorization
By using the relation between zeroes and coefficients, we have alpha beta gamma = 0/k = 0 alpha beta gamma = 9/k Therefore, alpha 3 If the square difference of the quadratic polynomial is the zeroes of p(x)=x^23x k is 3 then find the value of k;Get sum, product, and sum of products of pairs of roots for original polynomial, eg {αβ = ⁻ᵇ/ₐ ;



Link Springer Com




If Alpha Beta And Gamma Are The Zeroes Of Cubic Polynomial Kx3 5x
Finding a cubic polynomial whose zeroes are the same as collectively of two other quadratic polynomials 1 Given some zeroes of a real polynomial of a given degree, how can one find the remaining zeroes?Click here👆to get an answer to your question ️ If alpha, beta and gamma are zeros of the polynomial 6x^3 3x^2 5x 1 , then find the value of alpha^1 beta^1 gamma^1Advertisement Remove all ads
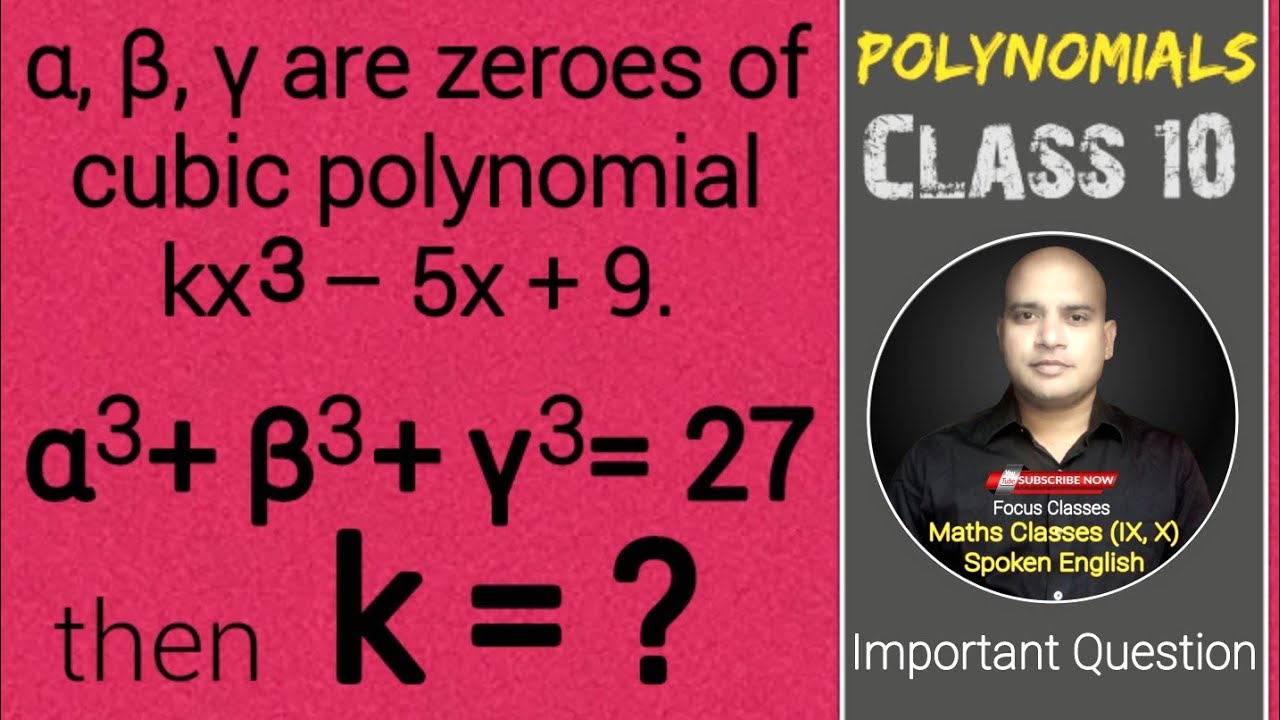



A B G Are Zeroes Of Cubic Polynomial Kx 3 5x 9 If A 3 B 3 G 3 27 Find The Value Of K Youtube




Math Physics Chemistry Questions Discussion Lists Dated 18 06 05
Q16 pl solve Q 16 α, β, γ are zeroes of cubic polynomial kx35x9 If α3β3γ3=27, find the value of k Maths PolynomialsI f α and β are the zeros of polynomial x2 5x k such that α β =1 find the value of k asked in Class X Maths by akansha Expert ( 78k points) 0 votesRD Sharma solutions for Class 10 Maths Chapter 2 PolynomialsExercise 22 Page 43 Verify that the numbers given along side of the cubic polynomials are their zeroes Also verify the relationship between the zeroes and the coefficients `2x^3 x^2 – 5x 2 ;




Math Physics Chemistry Questions Discussion Lists Dated 17 10 15




If Alpha Beta Gamma Zeros Cubic Polynomial Kx3 5x 9 Youtube
Hence, find the zeroes of the cubic polynomial x3 2x2 kx – 18 Solution Let p(x) = x3 2x2 kx 3 Then, p(3) = 33 2 × 32 3k 3 = 21 ie, 3k = –27 ie, k = –9 Hence, the given polynomial will become x3 2x2 – 9x 3Here is an example of a 3rd degree polynomial we can factor by first taking a common factor and then using the sumproduct pattern Α,β and γ are zeros of cubic polynomial and are in AP So, Let β=a ;



Intellect Guidance Centre Near Shiv Mandir Surendra Gali Jora Phatak More Dhansar Dhanbad Dhanbad 21



Xdocs Pl
POLYNOMIALS 9 Sample Question 2 Given that two of the zeroes of the cubic polynomial ax3 bx2 cx d are 0, the third zero is (A) –b a (B) b a c a (D) – d a Solution Answer (A)Hint Because if third zero is α, sum of the zeroes= α 0 0 = –b a EXERCISE 21 Choose the correct answer from the given four options in the following questions1/2, 1, – 2`If α, β and γ are zeroes of the polynomial 6x^3 3x^2 5x 1, then find the value of α^1 β^1 γ^1 asked in Mathematics by AnjaliVarma ( 294k points) polynomials




Alpha Beeta And Gamma Are Zeroes F The Cubic Polynomial X3 2x2 Qx R If Alpha Beta 0 Then Show Maths Polynomials Meritnation Com




Intellect Guidance Centre Posts Facebook
Answer (1 of 12) Vieta's Formulas tell us the sum of the roots, \alpha \beta, is \frac{5}{1}=5 From the question, \alpha \beta = 1 We can solveIf α, β are the zeros of the polynomial f(x) = x 2 – 5x k such that α ‒ β = 1, find the value of k Answer It is given in the question that, f (x) = x 2 – 5x k such that its coefficients are a = 1, b = 5 and c = k ∴ = = 5 (i), = 1 (ii), we get 2α = 6 α = = 3 Now putting the value ofQ9 If α and β are zeros of p(x) = x2 x1, then find 1/α 1/β?



Gisk Gajeratrust Org




If Alpha Beta And Gama Are The Zeros Of The Polynomial Ax3 Bx2 Cx D Find The Value Of 1 Alpha 2 1 Beta 2 1 Gama2 Mathematics Topperlearning Com Ykycwpyy
11 If α and β are the zeroes of x 2 px q then find the value of (3 marks) 12 Find the zeroes of 2x 2 – 8x 6 (3 marks) 13 Find the value of 'k' such that the quadratic polynomial 3x 2 2kx x – k – 5 has the sum of zeroes as half of their product (3 marks) 14 Find the cubic polynomial whose zeroes are 5, 3 and –2 (3 If α, β and γ are the zeroes of cubic polynomial kx 3 5x 9 and α 3 β 3 γ 3 = 27, then find the value of k If one zero of the polynomial 3x 2 – 8x 2k 1 and seven times the other, find the value of k Answer Let α and β be the zeroes of the polynomial Then as per question β = 7α Now sum of zeroes = α β = α 7α Question 14 If one zero of polynomial (a 2 9)x 2 13x 6a and reciprocal of the other, find the value of a Answer




If A Ss And Y Are The Zeroes Of Cubic Polynomialkx3 5x 9 And A3 73 27 Then Find Thevalue Brainly In




Q16 Pl Solve Q 16 A B G Are Zeroes Of Cubic Polynomial Kx3 5x 9 If A3 G3 27 Maths Polynomials Meritnation Com
Given that two of the zeroes of the cubic polynomial ax 3 bx² cx d are 0, the third zero is Answer Answer a 3 If one of the zeroes of the quadratic polynomial (k – 1) x² kx 1 is – 3, then the value of k is Answer Answer a 4 A quadratic polynomial, whose zeroes are



Ayazsir Com




Alpha Beta Gamma Are Zeroes Of Cubic Polynomial K X 3 5 X 9 If Alpha 3 Beta 3 Gamma 3 27 Find The Value Of K




A B Y Are Zeroes Of Cubic Polynomial Kx3 5x 9 If A3 Y3 27 Fi




Chapter 1 Introduction




If A B C Are The Zeroes Of Cubic Polynomial Kx3 5x 9 And A3 C3 27 Then Find The Brainly In



Xdocs Pl




Polynomials 1 Pdf Polynomial Factorization




Intellect Guidance Centre Posts Facebook




Math Physics Chemistry Questions Discussion Lists Dated 18 06 05




If Alpha Beta And Gamma Are The Zeroes Of Cubic Polynomial Kx3 5x



Pisnandedstd10home Files Wordpress Com




If Alpha Beta And Gamma Are The Zeroes Of The Polynomial And Alpha 3 Beta 3 Gamma 3 27 Youtube




A B G Are Zeroes Of Cubic Polynomial Kx 3 5x 9 If A 3 B 3 G 3 27 Find The Value Of K Youtube



Olterus Com




Intellect Guidance Centre Near Shiv Mandir Surendra Gali Jora Phatak More Dhansar Dhanbad Dhanbad 21




Intellect Guidance Centre Posts Facebook




Intellect Guidance Centre Posts Facebook




Intellect Guidance Centre Posts Facebook




If Alpha Beta And Gama Are Zeros Of Polynomial 6x3 3x2 5x 1 Then Find Value Of Alpha Di Power 1 Beta Brainly In




A B G Are Zeroes Of Cubic Polynomial Kx3 5x 9 If A3 G3 27 Find The Value Of Brainly In



Pisnandedstd10home Files Wordpress Com



Xdocs Pl




Alpha Beta Gamma Are The Zero Of Cubic Polynomial Kx 3 5x 9 If Alpha 3 Beta 3 Gamma 3 27 Find The Brainly In




Preview Cambridge International As And A Level Pure Mathematics 2 3 By Cambridge University Press Education Issuu



If Alpha Beta Gamma Are Zeros Of Cubic Polynomial X 3 5x 2 What Is The Value Of Alpha 3 Beta 3 Gamma 3 Quora




If Alpha Beta And Gamma Are The Zeroes Of The Polynomial And Alpha 3 Beta 3 Gamma 3 27 Youtube




Q1 If Alpha And Beta Are Zeroes Of The Quadratic Polynomial F X 3x Sup2 5x 2 Then Evaluate Alpha Sup3 Beta Sup3 Q2 If One Of The Zeroes Of The Cubic




Polynomials Pdf Quadratic Equation Polynomial




Alpha Beta Gamma Are The Zeroes Of Cubic Polynomial P X Ax 3 Bx 2 Cx D A 0 Then Product Of Their Zeroes Alpha Beta Gamma




Cbse Maths 10 Mcqs Standard Levels Choose Class Mathematics Pubhtml5
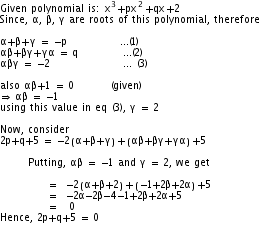



If Alpha Beta Gamma Are Zeros Of The Polynomial X3 Px2 Qx 2 Such That Alpha Beta 1 0 Find The Value Of 2p Q 5 Mathematics Topperlearning Com 44x9hrnn



New Pubhtml5 Com



Dvmsohna Com



If A B And G Are Zeroes Of The Polynomial 6x 3 3x 2 5x 1 Then Find The Value Of A 1 B 1 G 1 Sarthaks Econnect Largest Online Education Community




Sir If Alpha Beeta Gamma Are Zeroes Of Polynomials F X 2x 3 6x 2 4x 9 Find The Value Of 1 Alphabeeta 1 Beetagammma 1 Gamma Alpha Mathematics Topperlearning Com Eowyxlzz




If Alpha Beta Gamma Are Zeros Of Cubic Polynomial X 3 5x 2 What Is The Value Of Alpha 3 Beta 3 Gamma 3 Quora




A B Y Are The Zeroesof Cubic Polynomial Kx3 5x 9 Ifa3 Y3 27




Cbse Maths 10 Mcqs Standard Levels Choose Class Mathematics Pubhtml5



If Alpha Beta Gamma Are Zeros Of Cubic Polynomial X 3 5x 2 What Is The Value Of Alpha 3 Beta 3 Gamma 3 Quora




Polynomials Pdf Quadratic Equation Polynomial




Alpha Beta Gamma Are Zeros Of A Cubic Polynomial Kx Cube Minus 5 X 9 If Alpha Cube Beta Cube Plus Brainly In




If Alpha Beta And Gamma Are The Zeroes Of Cubic Polynomial Kx3 5x



Researchgate Net




Alpha Beta Gamma Are Zeroes Of Cubic Polynomial K X 3 5 X 9 If Alpha 3 Beta 3 Gamma 3 27 Find The Value Of K




Polynomials Pdf Quadratic Equation Polynomial




A B G Are Zeroes Of Cubic Polynomial Kx 3 5x 9 If A 3 B 3 G 3 27 Find The Value Of K Youtube




If Alpha Beta Gamma Are Zeroes Of Cubic Polynomial X 3 5x 2 Then Find The Value Of Youtube




Intellect Guidance Centre Near Shiv Mandir Surendra Gali Jora Phatak More Dhansar Dhanbad Dhanbad 21




If Alpha And Beta Are The Zeros Of The Polynomial 2x 2 5x 7 Then 2alpha 3beta And 3alpha 2beta Youtube




Q11 If A B And G Are The Zeroes Of The Cubic Polynomial P X 3x 6x 5x 3 Then Find Their Brainly In



Ayazsir Com



Kiitworld In



If The Zeroes Of The Cubic Polynomial X 3 3x 2 Kx 3 Are Alpha Beta Alpha Alpha Beta Then Find The Value Of Alpha Beta And K Plz Help Me With This Alpha 1 Beta 2 K 1
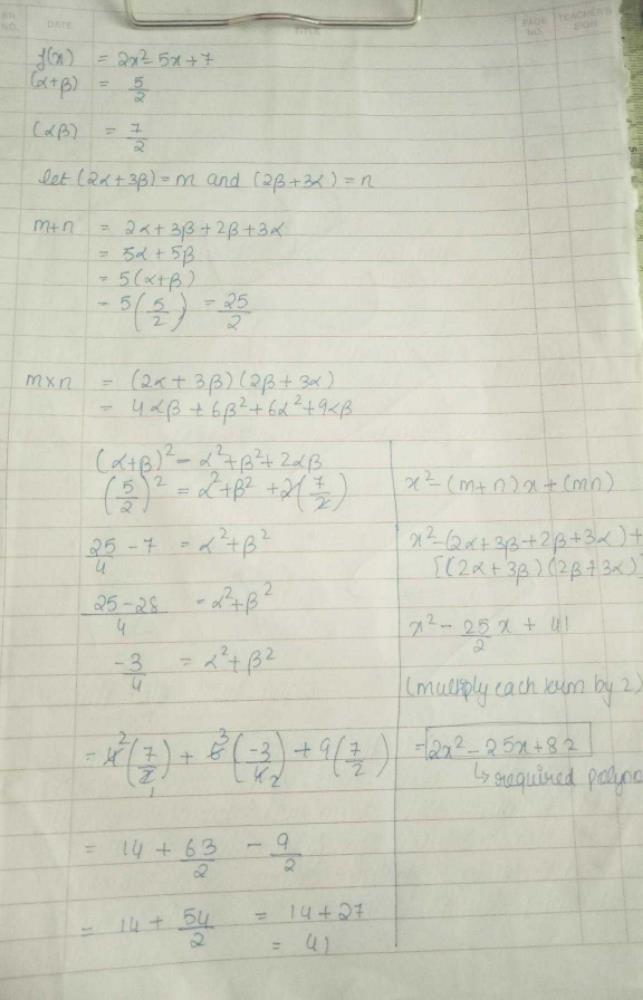



If Alpha And Beta Are The Zeros Of The Polynomial 2x 2 5x 7 Then Find The Polynomial Whose Zeros Are 2alpha 3beta And 3alpha 2beta Pls Answer With Solution Edurev Class 10 Question




Math Physics Chemistry Questions Discussion Lists Dated 18 05 01



Jfac Kr



Ayazsir Com



Link Springer Com




If Alpha Beta Gamma Are Zeros Of Cubic Polynomial X 3 5x 2 What Is The Value Of Alpha 3 Beta 3 Gamma 3 Quora




Intellect Guidance Centre Near Shiv Mandir Surendra Gali Jora Phatak More Dhansar Dhanbad Dhanbad 21




If Alpha Beta And Gamma Are The Zeroes Of The Polynomial And Alpha 3 Beta 3 Gamma 3 27 Youtube




If Alpha Beta Gamma Are Zeroes Of Polynomial X 3 2x 2 Qx R 0 Alpha Beta 0 Then Show 2q R Youtube




If A B And G Are The Zeroes Of Cubic Polynomial Kx3 5x 9 And A3 Maths Real Numbers Meritnation Com



Link Springer Com



Link Springer Com




Preview Cambridge International As And A Level Pure Mathematics 2 3 By Cambridge University Press Education Issuu




Cbse Maths 10 Mcqs Standard Levels Choose Class Mathematics Pubhtml5




Most Important Questions For Cbse Class 10th




Polynomials Pdf Quadratic Equation Polynomial




Polynomials Pdf Quadratic Equation Polynomial




If Alpha Beta And Gamma Are The Zeros Of The Cubic Polynomial Ax Cube B X Square 5 Maths Polynomials Meritnation Com




Questions For Grade 10 Physics Pdf Polynomial Fraction Mathematics



0 件のコメント:
コメントを投稿